Trong hình học tập, góc là 1 đối tượng người dùng hình học tập được khái niệm với nhì tia đem điểm cuối cộng đồng. Hai tia này được gọi là tâm của góc còn điểm cuối cộng đồng của bọn chúng được nghĩ rằng đỉnh của chính nó. Các góc này được xác lập phía trên mặt mũi bằng phẳng Euclide, tuy vậy một trong những góc cũng rất có thể được phân biệt nhập hình học tập Euclid.
1.1 Định nghĩa và đặc điểm của 2 góc đồng vị:
Nếu đường thẳng liền mạch t hạn chế hai tuyến đường trực tiếp f và r và trong số góc tạo nên trở thành đem một cặp góc đồng vị cân nhau thì những cặp góc đồng vị không giống cũng vì như thế nhau:
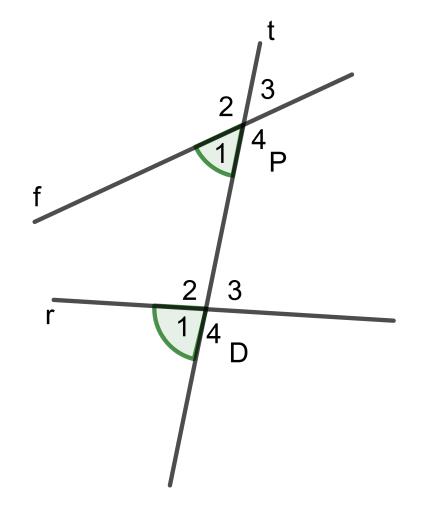
Hai góc P1 và D1 được gọi là nhì góc đồng vị
Ta rất có thể hiểu nhì góc đồng vị là nhì góc nằm tại địa điểm giống như nhau.
Có thể rút rời khỏi tín hiệu cơ bạn dạng nhằm nhận ra quan hệ góc này là:
Hai góc ko cộng đồng gốc.
Hai góc nằm tại và một phía đối với đường thẳng liền mạch hạn chế và nằm tại địa điểm giống như nhau bên trên 2 đường thẳng liền mạch tuy vậy tuy vậy.
Nếu đường thẳng liền mạch c hạn chế hai tuyến đường trực tiếp a, b và trong số góc tạo nên trở thành mang 1 cặp góc ví le nhập cân nhau thì:
– Hai góc ví le nhập sót lại vì như thế nhau
– Hai góc đồng vị vì như thế nhau
1.2. Phương pháp nhận ra nhì góc đồng vị:
Để nhận ra nhì góc đồng vị, tao phụ thuộc vào những tín hiệu sau:
Cho đường thẳng liền mạch t hạn chế hai tuyến đường trực tiếp u và v tạo nên trở thành những góc. Khi cơ những cặp góc đồng vị đem những điểm sáng sau:
– Hai góc ko được cộng đồng gốc
– Hai góc cơ nên ở và một phía đối với đường thẳng liền mạch t và nằm tại địa điểm giống như nhau bên trên hai tuyến đường trực tiếp u và v
1.3 Các dạng bài bác luyện về góc đồng vị:
Dạng bài bác luyện 1: Nhận biết nhì góc đồng vị. Phương pháp giải của dạng bài bác luyện này là phụ thuộc vào khái niệm góc đồng vị.
Dạng bài bác luyện 2: Tính số đo của những góc tạo nên trở thành từ 1 đường thẳng liền mạch hạn chế hai tuyến đường trực tiếp tuy vậy tuy vậy. Phương pháp giải của dạng bài bác luyện này là vận dụng những đặc điểm của góc đồng vị (hai góc đồng vị vì như thế nhau) nhằm lần rời khỏi phía đo lường và tính toán hợp lý và phải chăng.
Dạng bài bác luyện 3: Chứng minh hai tuyến đường trực tiếp tuy vậy tuy vậy. Dựa nhập quyết định lý hòn đảo góc đồng vị, nếu mà một đường thẳng liền mạch hạn chế hai tuyến đường trực tiếp bất kì, nhì góc ở địa điểm đồng vị cân nhau thì minh chứng hai tuyến đường trực tiếp cơ tuy vậy tuy vậy.
2. Góc ví le nhập là gì?
2.1. Góc ví le nhập là gì?
Định nghĩa góc ví le trong: Giả sử mang 1 đường thẳng liền mạch t hạn chế đường thẳng liền mạch q tạo nên trở thành tư góc và hạn chế đường thẳng liền mạch r tạo nên trở thành tư góc. Khi cơ nhì góc ví le nhập là nhì góc ko đỉnh chung, nằm tại bên phía trong hai tuyến đường trực tiếp q và r và nằm tại không giống phía đối với đường thẳng liền mạch t.
Ví dụ:
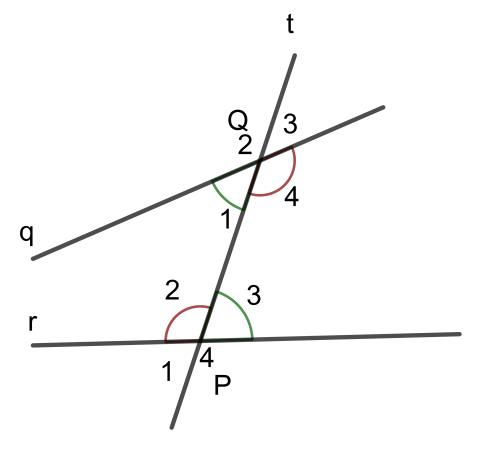
Góc Q1 và góc P3 là nhì góc ví le trong
Tương tự động, góc Q4 và góc P2 là nhì góc ví le trong
2.2. Tính chất:
Nếu lối thẳng cc cắt hai tuyến đường thẳng aa và bb, trong số góc tạo nên trở thành mang 1 cặp góc ví le nhập cân nhau thì:
a) Hai góc ví le nhập sót lại cân nhau.
b) Hai góc đồng vị (trong từng cặp) cân nhau.
c) Hai góc nhập nằm trong phía bù nhau
Cụ thể như sau:
Từ hình vẽ bên trên, tao thấy những góc Q3, Q4, P1, P2 là những góc nằm tại phía nhập hai tuyến đường trực tiếp u và v.
Góc Q1 và P3 là nhì góc ko cộng đồng gốc, nằm tại không giống phía đối với đường thẳng liền mạch t nên góc P1 và T3 là nhì góc ví le nhập.
Tương tự động, tao đem góc Q4 và P2 là nhì góc ko cộng đồng gốc, nằm tại không giống phía đối với đường thẳng liền mạch t nên góc Q4 và P2 là nhì góc ví le nhập.
Còn góc Q1 và P2, Q4 và P3 cũng là những cặp góc ko cộng đồng gốc tuy nhiên ở và một phía với đường thẳng liền mạch q nên những cặp góc cơ ko nên là góc ví le nhập.
2.3 Dấu hiệu nhận ra nhì góc ví le trong:
Cho đường thẳng liền mạch t hạn chế hai tuyến đường trực tiếp q và r tạo nên trở thành những góc. Khi cơ nhằm nhận ra được nhì góc ví le nhập, tao phụ thuộc vào những tín hiệu sau:
– Hai góc ko được cộng đồng gốc
– Hai góc cơ nên nằm tại phía nhập hai tuyến đường trực tiếp q và r.
– Hai góc cơ nên nằm tại địa điểm ví le nhau, hoặc thưa cách thứ hai, nhì góc cơ nên nằm tại không giống phía đối với đường thẳng liền mạch t.
3. Góc nằm trong phía là gì?
3.1. Định nghĩa:
Giả sử mang 1 đường thẳng liền mạch d bất kì hạn chế đường thẳng liền mạch q và t tạo nên trở thành những góc. Khi cơ nhì góc nhập nằm trong phía là nhì góc ko đỉnh chung, nằm tại phía bên phía trong hai tuyến đường trực tiếp q và t và nằm tại và một phia đối với đường thẳng liền mạch d.
*Nhận xét: Nếu đường thẳng liền mạch d hạn chế hai tuyến đường trực tiếp q và t tuy nhiên q và t tuy vậy song cùng nhau thì các góc nhập nằm trong phía tiếp tục bù nhau. Khi đó tổng số đo của nhì góc nhập nằm trong phía tiếp tục vì như thế 180o.
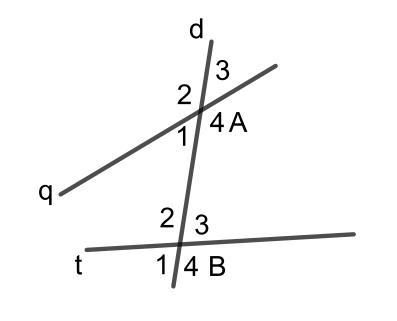
Từ hình vẽ bên trên, tao thấy góc A1 và góc B2 là nhì góc nhập nằm trong phía.
Tương tự động như thế, tao cũng có thể có góc A4 và B3 là nhì góc nhập nằm trong phía.
3.2. Cách nhận ra góc nhập nằm trong phía:
Giả sử mang 1 đường thẳng liền mạch d hạn chế đường thẳng liền mạch q bên trên B và hạn chế đường thẳng liền mạch t bên trên F tạo nên trở thành những góc đỉnh B và đỉnh F. Khi cơ nhằm hiểu rằng nhì góc thế nào là nhì góc nhập nằm trong phía tao phụ thuộc vào những điểm sáng sau:
Hai góc cơ ko cộng đồng gốc. Có nghĩa là 1 góc đỉnh B và một góc đỉnh F.
Hai góc này đều nằm tại phía nhập đối với hai tuyến đường trực tiếp q và t.
Hai góc cơ nằm tại địa điểm và một mặt mũi đối với đường thẳng liền mạch d. Hay thưa cách thứ hai, nhì góc cơ nên nằm tại nằm trong phía đối với đường thẳng liền mạch d.
4. Các dạng bài bác luyện thông thường gặp:
–Dạng 1: Xác quyết định những cặp góc ví le nhập, cặp góc đồng vị, cặp góc nhập nằm trong phía.
– Dạng 2: Tính số đo góc lúc biết 1 trong tư góc tạo nên vì như thế hai tuyến đường trực tiếp.
– Dạng 3: Tìm những cặp góc cân nhau, cặp góc bù nhau.
– Dạng 4: Xác xác định trí của những góc.
– Dạng 5: Chứng minh địa điểm của những góc.
– Dạng 6: Tìm những cặp góc vừa lòng ĐK bài bác cho tới.
– Dạng 7: Ứng dụng địa điểm của góc nhập những câu hỏi khác: tam giác, hình vuông vắn, hình tròn trụ.
5. Phương pháp giải những bài bác luyện về góc và ví dụ minh họa:
Để giải chất lượng câu hỏi tính số đo góc thì người học tập trước không còn nên nắm rõ kỹ năng và kiến thức cơ bạn dạng sau về góc và những quan hệ nhập góc như sau:
* Trong tam giác:
+ Tổng phụ vương góc nhập bằng 180°.
+ Khi biết nhì góc tất cả chúng ta xác lập được góc sót lại.
* Trong tam giác cân: Biết một góc tất cả chúng ta xác lập được nhì góc sót lại.
* Trong tam giác vuông:
+ thạo một góc nhọn, tất cả chúng ta xác lập được góc nhọn sót lại.
+ Cạnh góc vuông vì như thế nửa cạnh huyền thì góc đối lập với cạnh góc vuông cơ đem số đo bằng 30°30°.
* Trong tam giác vuông cân: Mỗi góc nhọn đem số đo bằng 45°45°.
* Trong tam giác đều: Mỗi góc đem số đo bằng 60°.60°.
* Đường phân giác của một góc phân chia góc cơ rời khỏi nhì góc đem số đo cân nhau.
* Hai lối phân giác của nhì góc kề bù thì vuông góc cùng nhau.
* Hai góc đối đỉnh thì cân nhau.
* Tính hóa học về góc ví le nhập, đồng vị, nhập nằm trong phía, của một đường thẳng liền mạch hạn chế hai tuyến đường trực tiếp tuy vậy tuy vậy.
Trong thực tiễn, nhằm giải câu hỏi tính số đo góc, tao thông thường xét những góc cơ trực thuộc côn trùng contact với những góc ở những hình đặc biệt quan trọng đang được nêu phía trên hoặc xét những góc ứng cân nhau,. .. rồi tiếp sau đó tiếp tục suy được rời khỏi sản phẩm.
Ví dụ minh họa 1: Nếu hai tuyến đường trực tiếp c hạn chế hai tuyến đường trực tiếp a,b và trong số góc tạo nên trở thành mang 1 cặp góc ví le nhập cân nhau thì:
A. Hai góc nhập nằm trong phía vì như thế nhau
B. Hai góc đồng vị vì như thế nhau
C. Hai góc ví le nhập sót lại đem tổng bằng 120°
D. Tất cả những đáp án bên trên đều đúng
Đáp án nên chọn là: B
Nếu lối thẳng c cắt hai tuyến đường thẳng a, và trong số góc tạo nên trở thành mang 1 cặp góc ví le nhập cân nhau thì: nhì góc đồng vị vì như thế nhau
Ví dụ minh họa số 2: Nếu hai tuyến đường trực tiếp c hạn chế hai tuyến đường trực tiếp a,b và trong số góc tạo nên trở thành mang 1 cặp góc đồng vị cân nhau thì:
A. Hai góc nhập nằm trong phía vì như thế nhau
B. Hai góc ví le nhập bù nhau
C. Hai góc nhập nằm trong phía bù nhau
D. Tất cả những đáp án bên trên đều đún
Đáp án nên chọn là: C
Đường trực tiếp c hạn chế hai tuyến đường trực tiếp a,b ứng bên trên A,B và trong số góc tạo nên trở thành mang 1 cặp góc đồng vị cân nhau, fake sử
+ Xét một cặp góc nhập nằm trong phía, chẳng hạn
Do cơ nhì góc nhập nằm trong phía bù nhau nên A sai, C đúng
Vậy nhì góc ví le trong cân nhau. Đáp án B sai